hckim

풀이

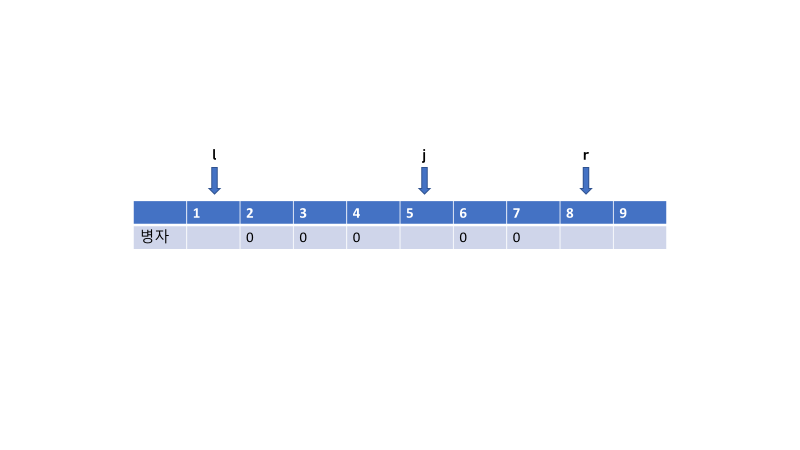
• 인접한 땅과 땅사이 이동은 비용없이 가능
• 점프 단 한번 할 수 있는데 i, i + x 점프 비용 x
• 물 없으면 비용 0 으로 갈 수 있고 물이 있으면 점프를 첫부분과 연결된 땅의 오른쪽 끝에서 시작하여 , 끝부분과 연결된 땅의 왼쪽끝에서 도착하는 것이 최적이다.

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
 
    int TC; cin >> TC;
    while (TC--) {
        int N;
        cin >> N;
 
        vector<int> a(N);
        long long ans = 0;
        for (int i = 0; i < N; ++i) {
            cin >> a[i];
        }
 
        int i = 0;
        while (i < N - 1) {
            if (a[i + 1] == 0) {
                break;
            }
            ++i;
        }
        if (i == N - 1) {
            cout << "0\n";
            continue;
        }
 
        int j = N - 1;
 
        while (j > 0) {
            if (a[j - 1] == 0) {
                break;
            }
            --j;
        }
 
        cout << j - i << '\n';
    }
 
}

풀이

• 패스 수 대로 배열 정렬
• 1, 2, 3, ... , n 번 그룹에서 n 번 공 가지고 출발해서 앞번호로 차례로 패스, n 번 마지막으로 공가져간다고 하면
• a[n] <= sum(a[1] ... a[n - 1]) 일 때 1개의 공으로 다 처리 가능,
  • 1번 0 될 때까지 1, ... n 그룹 패스
  • 2번 0 될 때까지 2, ... n 그룹 패스
• a[n]  이 클 때는 큰만큼 추가 공 필요

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        int N;
        cin >> N;
 
        vector<long long> a(N);
        long long sum = 0;
        for (auto & e : a) {
            cin >> e;
            sum += e;
        }
        sort(all(a));
        if (a.back() == 0) {
            cout << "0\n";
            continue;
        }
 
        long long ans = 1;
        if (sum - a.back() < a.back()) {
            ans = a.back() - sum + a.back();
        }
 
        cout << ans << '\n';
    }
}

풀이

• 하나의 color 에 대해서
  • x 좌표들에 대해서
    • 그 x 좌표가 정답에 더해지는 부분은 그 좌표보다 작은 부분들 - 그 x 좌표 

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
 
    map<int, map<int, int> > mr;
    map<int, map<int, int> > mc;
    set<int> colors;
    int N, M;
    cin >> N >> M;
 
 
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < M; ++j) {
            int c;
            cin >> c;
            colors.insert(c);
            ++mr[c][i];
            ++mc[c][j];
        }
    }
 
    long long ans = 0;
    for (auto c: colors) {
        long long tmp = 0;
        long long tmpCnt = 0;
        for (auto it = mr[c].begin(); it != mr[c].end(); ++it) {
            ans += (it -> first * tmpCnt - tmp) * it -> second;
            tmp += it -> first * it -> second;
            tmpCnt += it -> second;
        }
 
        tmp = 0;
        tmpCnt = 0;
        for (auto it = mc[c].begin(); it != mc[c].end(); ++it) {
            ans += (it -> first * tmpCnt - tmp) * it -> second;
            tmp += it -> first * it -> second;
            tmpCnt += it -> second;
        }
    }
    cout << ans << '\n';    
}

풀이

• 몫의 범위는 0 ~ C
• 지금 배열안에 존재하지 않는 값에 대하여, 그 값이 몫으로 나올 수 있는지 체크
• 모든 배열 원소에 대하여, 원소 값을 x 라 하면, x * c ~ x * (c + 1) 사이에 값이 있으면 몫으로 그 값이 나올 수 있겠다.
• c 는 0~C 까지 돌려야되고 x 는 x * c <= C 까지만 돌려도 되므로
• 시간 복잡도 계산은 C + C/ 2 + C / 3 ...  = ClogC

코드

• 시간복잡도: $O(ClogC)$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        int N, C;
        cin >> N >> C;
 
        vector<int> exist(C + 1, false);
        vector<int> a(N);
        for (auto& e: a) {
            cin >> e;
            exist[e] = true;
        }
 
        vector<int> pe(C + 1, 0);
        for (int i = 1; i < C + 1; ++i) {
            pe[i] = pe[i - 1] + exist[i];
        }
 
        bool yes = true;
        for (int i = 1; i <= C; ++i) {
            if (exist[i]) continue;
            for (int j = 1; j * i <= C; ++j) {
                if (!exist[j]) continue;
                // i not exist, j exist, check exist something / j = i
                if (pe[min(C, j * (i + 1) - 1)] - pe[j * i - 1]) {
                    yes = false;
                    break;
                }
            }
            if (!yes) break;
        }
 
        if (yes) {
            cout << "Yes\n";
        } else {
            cout << "No\n";
        }
    }
}

풀이

• j = 0 ... i -1 에서 s[j] = t[j] 이고, s[i] < t[i] 인 개수 를 i가 0 ... m 일 때 더해주면 답이다.

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    long long N, M;
    cin >> N >> M;
 
    vector<long long> s(N), t(M);
    vector<long long> t2(2 * 200001, 0);
    vector<long long> fact(200001, 1LL);
    long long MOD = 998244353;
    for (long long i = 1; i < fact.size(); ++i) {
        fact[i] = i * fact[i - 1] % MOD;
    }
 
    auto fpow = [&](long long base, long long p) {
        long long ret = 1;
        while (p) {
            if (p & 1) {
                ret = ret * base % MOD;
            }
            base = base * base % MOD;
            p >>= 1;
        }
        return ret;
    };
 
    int n = 200001;
    long long div = 1;
 
    for (auto& e: s) {
        cin >> e;
        ++t2[n + e];
    }
 
    for (long long i = 1; i <= 200000; ++i) {
        if (t2[n + i]) {
            div = div * fpow(fact[t2[n + i]], MOD - 2) % MOD;
        }
    }
 
    for (auto& e: t) {
        cin >> e;
    }
 
    for (int i = n - 1; i >= 1; --i) {
        t2[i] = t2[i << 1] + t2[i << 1 | 1];
    }
 
    auto query = [&](int l, int r) {
        long long ret = 0;
        for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
            if (l & 1) ret += t2[l++];
            if (r & 1) ret += t2[--r];
        }
        return ret;
    };
 
    auto update = [&](int p, int val) {
        for (t2[p += n] = val; p > 1; p >>= 1) t2[p >> 1] = t2[p] + t2[p ^ 1];
    };
 
    long long ans = 0;
    for (int i = 0; i < M; ++i) {
        ans += div * fact[N - i - 1] % MOD * query(0, t[i]) % MOD;
        ans %= MOD;
 
        if (t2[n + t[i]]) {
            div = div * t2[n + t[i]] % MOD;
            update(t[i], t2[n + t[i]] - 1);
        } else {
            if (i >= N) ans += 1, ans %= MOD;
            break;
        }
    }
    cout << ans << '\n';
}

풀이

• n + 1 개 중 $a[i] = n^2 $인 원소의 개수를 x 라 하면
• $s = x * n^2 + R$ 이고 $R = (n + 1 - x) * (0...n - 1)$ 이다
• R 의 최대가 $n^2 - 1$ 이므로 
• 구하는 답은 $ S / N^2 $ 이다

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
 
    int TC; cin >> TC;
    while (TC--) {
        long long N, S;
        cin >> N >> S;
 
        cout << S / (N * N) << '\n';
    }
}

풀이

• 빨간색 개수보다 파란색 개수가 한개 더 많은 것이 개수 조건을 만족하면서, 합조건을 만족하기에 최선이다.
• 파란색 집합에는 작은것, 빨간색 집합에는 큰것이 들어가는 것이 합조건을 만족하기에 최선이다.
• 배열 오름차순 정렬후 파란색을 앞에서부터, 빨간색을 뒤에서부터 개수 증가시켜가면서 조건 만족하는 것 있는지 찾기

코드

• 시간복잡도: $O(NlogN)$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        int N;
        cin >> N;
        vector<long long> a(N), pa(N, 0);
        for (int i = 0; i < N; ++i) {
            cin >> a[i];
        }
        sort(all(a));
        for (int i = 0; i < N; ++i) {
            pa[i] = a[i];
            if (i) pa[i] += pa[i - 1];
        }
        
 
        bool yes = false;
        for (int i = 2; i < N; ++i) {
            if (i + i - 1 > N) break;
            if (pa[i - 1] < pa[N - 1] - pa[N - i]) {
                yes = true;
                break;
            }
        }
 
        if (yes) {
            cout << "YES\n";
        } else {
            cout << "NO\n";
        }
    }
}

풀이

• powerful number 는 겹치지 않는 두 집합으로 나눌 수 있다.
  • $2^d$ : $1, 2, 4, 8, ... $
  • $3!, 4!, 5!, ...$
• $10^{12}$ 를 넘지 않는 팩토리얼은 $14!$ 이므로 모든 조합의 수는 $2^{12} - 1$ 이다.
• N 넘지 않는 모든 팩토리얼 합에 대해서 개수를 구해주고 최소를 구하면 된다.

코드

• 시간복잡도: $O(2^{12})$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    vector<long long> fac(15, 1);
    for (int i = 1; i < 15; ++i) {
        fac[i] = fac[i - 1] * i;
    }
    
    int TC; cin >> TC;
    while (TC--) {
        long long N;
        cin >> N;
        long long ans = 1e9;
        for (long long i = 0; i < (1 << 12); ++i) {
            long long cnt1 = 0, cnt2 = 0;
            long long factSum = 0;
 
            for (long long j = 0; j < 12; ++j) {
                if (i & (1LL << j)) {
                    factSum += fac[j + 3];
                    ++cnt1;
                }
            }
 
            long long tmp = N - factSum;
            if (tmp < 0) break;
            while (tmp) {
                if (tmp & 1) ++cnt2;
                tmp >>= 1;
            }
 
            ans = min(ans, cnt1 + cnt2);
        }
        cout << ans << '\n';
    }
}

풀이

• N = 2 인 경우를 제외하고, 한 간선의 양 끝 정점이 모두 good 일 수 없다.
• not good 일 때는 value 가 1 일 때 최소 합을 가진다.
• $dp[i][g]: $ i 정점이 good: g 이고 i 루트로 가지는 서브트리의 {최대 good 개수, 최소 합} 으로 정의
• $dp[i][g]$ 를 구할 때 g 가 true 이면( good 이면) 그 아래 정점들은 무조건 not good 이지만, g 가 false 면 그 아래 정점들이 good, not good 두가지 모두 따져야 원하는 dp 값을 구할 수 있다.

코드

• 시간복잡도:$O(N)$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int N;
    cin >> N;
 
    if (N == 2) {
        cout << "2 2\n";
        cout << "1 1\n";
        return 0;
    }
    vector<vector<int> > adj(N + 1);
 
    for (int i = 0; i < N - 1; ++i) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
 
    vector<vector<pair<int, int> > > dp(N + 1, vector<pair<int, int> > (2, {-1, -1}));
    function<pair<int, int>(int, int, int)> f = [&](int cur, int g, int p) {
        auto& ret = dp[cur][g];
 
        if (ret.first != -1) {
            return ret;
        }
 
        if (g) {
            ret = {g, -adj[cur].size()};
            for (auto e: adj[cur]) {
                if (e == p) continue;
                ret.first += f(e, !g, cur).first;
                ret.second += f(e, !g, cur).second;
            }
        } else {
            // not good
            ret = {g, -1};
            for (auto e: adj[cur]) {
                if (e == p) continue;
                if (f(e, g, cur) > f(e, !g, cur)) {
                    ret.first += f(e, g, cur).first;
                    ret.second += f(e, g, cur).second;
                } else {
                    ret.first += f(e, !g, cur).first;
                    ret.second += f(e, !g, cur).second;
                }
            }
        }
 
        return ret;
    };
 
    auto ans = max(f(1, 1, -1), f(1, 0, -1));
 
    cout << ans.first << ' ' << -ans.second << '\n';
    
    vector<int> w(N + 1, 0);
    function<void(int, int, pair<int, int>)> f2 = [&](int cur, int p, pair<int, int> val) {
        if (val == f(cur, 0, p)) {
            w[cur] = 1;
            for (auto e: adj[cur]) {
                if (e == p) continue;
                f2(e, cur, max(f(e, 0, cur), f(e, 1, cur)));
            }
        } else {
            w[cur] = adj[cur].size();
            for (auto e: adj[cur]) {
                if (e == p) continue;
                f2(e, cur, f(e, 0, cur));
            }
        }
 
    };
    f2(1, -1, ans);
    for (int i = 1; i <= N; ++i) {
        cout << w[i] << ' ';
    }
    cout << '\n';
}

풀이

• $x, x^2, ... , x^k$ 행들에서만 중복이 나올 수 있다. k 는 최대 $log_2 N$
• 각 행의 지수들은
  • $1 * 1, 1 * 2, ..., 1 * M$
  • $2 * 1, 2 * 2, ..., 2 * M$
  • $k * 1, k * 2, ..., k * M$
• k 에 따라 이 set 들에서의 distinct 한 개수가 정해진다.

코드

• 시간복잡도: $O(MlogN + N)$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int N, M;
    cin >> N >> M;
 
    vector<long long> cnt(log2(N) + 1, 0);
    vector<long long> checked((long long)(cnt.size()) * M, false);
    long long ccnt = 0;
    for (long long i = 1; i < cnt.size(); ++i) {
        for (long long j = 1; j <= M; ++j) {
            if (checked[i * j]) continue;
            checked[i * j] = true;
            ++ccnt;
        }
        cnt[i] = ccnt;
    }
 
    long long ans = 1;
    vector<int> counted(N + 1, false);
    for (long long i = 2; i <= N; ++i) {
        if (counted[i]) continue;
 
        long long tmp = i;
        long long k = 0;
        while (tmp <= N) {
            ++k;
            counted[tmp] = true;
            tmp *= i;
        }
 
        ans += cnt[k];
        counted[i] = true;
    }
    cout << ans << '\n';
}

풀이

• $y = 0$ 에 도달할 수 없는 점이 존재 하려면 세 점중 y 값이 최소가 아닌 두 점이 이루는 변이 x 축과 평행해야 하고 그 변의 길이가 답이 된다

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
 
        vector<pair<long long, long long> > p(3);
        for (int i = 0; i < 3; ++i) {
            cin >> p[i].first >> p[i].second;
        }
 
        if (p[0].second > p[1].second) swap(p[0], p[1]);
        if (p[0].second > p[2].second) swap(p[0], p[2]);
 
        long double answer = 0.0;
 
        if (p[1].second == p[2].second) {
            answer = abs(p[1].first - p[2].first);
        }
 
        cout.precision(9);
        cout << fixed << answer << '\n';
    }
}

풀이

• $k = n$ 일 때 힘의 합은 $k$
• $k = n - 1$ 일 때 서로 다른 두개를 합치면 합은 이전 합과 같고, 같은 두개 합치면 이전합 + 1 
• 같은 게 있으면 같은 것들 부터 합치자

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        int N;
        cin >> N;
        map<int, int> a;
        for (int i = 0; i < N; ++i) {
            int num;
            cin >> num;
            ++a[num];
        }
 
        int d = 0;
        for (auto [num, cnt]: a) {
            if (cnt >= 2) d += cnt - 1;
        }
 
        vector<int> answer;
        int k = N;
        for (int i = 0; i < N; ++i) {
            if (d) {
                answer.push_back(k);
                --k;
                d--;
            } else {
                answer.push_back(k);
            }
        }
 
        reverse(all(answer));
 
        for (auto e:answer) {
            cout << e << ' ';
        }
        cout << '\n';
        
    }
}

풀이

• 제일 큰 distinct 원소부터 매칭이 되면 넘어가고 수를 추가해야되면 그 수만큼 추가해준다

코드

• 시간복잡도: $O(NlogN)$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        long long N, X;
        cin >> N >> X;
        map<long long, long long> m;
        for (int i = 0; i < N; ++i) {
            int num;
            cin >> num;
            ++m[num];
        }
 
        int answer = 0;
        for (auto rit = m.rbegin(); rit != m.rend(); ++rit) {
            if (rit -> second == 0) continue;
            if (rit -> first % X == 0) {
                auto it = m.lower_bound(rit -> first / X);
                if (it != m.end() && it -> first == rit -> first / X && it -> second > 0) {
                    int tmp = min(rit -> second, it -> second);
                    it -> second -= tmp;
                    rit -> second -= tmp;
                }
 
                if (rit -> second > 0) {
                  answer += rit -> second;
                  rit -> second = 0;
                } 
            } else {
                answer += rit -> second;
            }
        }
        cout << answer << '\n';
    }
}

풀이

• operation 해도 각 문자들의 parity 가 유지되므로 홀수 개수인 문자가 존재하면 불가능하다
• 문자열 $c_1c_2c_3...$ 에 $c_3, c_2, c_1$ 을 뒤에 넣으면 $c_1c_2c_3c_3c_2c_1c_3c_2c_1...$ 로 만들 수 있다
• 앞에 부분은 tandem repeat 으로 빼놓고 뒷부분은 원래 문자열의 앞부분을 reverse 한것과 같다.
• 이 작업으로 문자열 뒷부분이 원래 문자열을 정렬한 상태로 두면 그 문자열은 순서대로 각 문자의 개수만큼 tandem repeat 을 이룬다
  • $c_1c_1c_2c_2c_2c_2c_3c_3...$

코드

• 시간복잡도: $O(N^2)$
  • 정렬하는데 각 원소마다 reverse 2번: $O(N)$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        int N;
        cin >> N;
        vector<long long> a(N);
        map<int, int> cnt;
        for (auto& e: a) {
            cin >> e;
            ++cnt[e];
        }
        bool no = false;
        for (auto e: cnt) {
            if (e.second & 1) {
                no = true;
                break;
            }
        }
 
        if (no) {
            cout << "-1\n";
            continue;
        }
 
        vector<long long> sortedA(a);
        sort(all(sortedA));
 
        int start = 0;
        vector<pair<int, int> > operation;
        vector<int> t;
 
        auto swapWithFirst = [&](int i) {
            if (i == 0) return;
            for (int j = 0; j <= i; ++j) {
                operation.push_back({start + j + i + 1, a[j]});
            }
            reverse(a.begin(), a.begin() + i + 1);
            t.push_back(i + 1 << 1);
            start += i + 1 << 1;
        };
        for (int i = N - 1; i > 0; --i) {
            if (a[i] != sortedA[i]) {
                auto it = find(a.begin(), a.begin() + i, sortedA[i]);
                if (it != a.begin()) {
                    swapWithFirst(it - a.begin());
                }
                swapWithFirst(i);
            }
        }
 
        for (auto e: cnt) {
            t.push_back(e.second);
        }
 
        cout << operation.size() << '\n';
        for (auto [p, c]: operation) {
            cout << p << ' ' << c << '\n';
        }
        cout << t.size() << '\n';
        for (auto e: t) {
            cout << e << ' ';
        }
        cout << '\n';
 
    }
}

풀이

• 병자 후보를 set 으로, 0 l r 1 쿼리를 세그먼트 트리로 관리
• t = 0 
  • x = 0
    • set 에서 l 부터 r 까지 범위에 있는것들 다 지움 ($O(NlogN)$)
  • x = 1
    • l 노드 값 min(t[N + l], r) 로 업데이트
• t = 1
  • 병자 후보에 없으면 병 안걸림
  • 병자 후보 set 에서의 j 의 위치 앞, 뒤에 있는 후보를 l, r 이라고 하면
  • l + 1, j 구간의 오른쪽 구간 최소값이 뒤 후보값인 r 보다 작으면 그 구간에 j가 1을 결정하므로 병자임을 확정할 수 있다. 그 외 경우엔 여러 원소가 있으므로 결정할 수 없다.

코드

• 시간복잡도: $O(NlogN + QlogN)$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int N, Q;
    cin >> N >> Q;
    
    set<int> can;
    for (int i = 0; i < N; ++i) can.insert(i);
    vector<int> t(2 * N, 1e9);
    auto update = [&](int p, int val) {
        for (t[p += N] = val; p > 1; p >>= 1) t[p >> 1] = min(t[p], t[p ^ 1]);
    };
    auto query = [&](int l, int r) {
        int ret = 1e9;
        for (l += N, r += N; l < r; l >>= 1, r >>= 1) {
            if (l & 1) ret = min(ret, t[l++]);
            if (r & 1) ret = min(ret, t[--r]);
        }
        return ret;
    };
 
    while (Q--) {
        int t2, l, r, x, j;
        cin >> t2;
        if (t2 == 0) {
            cin >> l >> r >> x; --l; --r;
            if (x == 0) {
                for (auto it = can.lower_bound(l); it != can.end() && r >= *it;) {
                    can.erase(it);
                    it = can.lower_bound(l);
                }
            } else {
                update(l, min(t[l + N], r));
            }
        } else {
            cin >> j; --j;
            if (!can.count(j) || !can.size()) {
                cout << "NO\n";
                continue;
            }
 
            int l = 0, r = N;
            auto it = can.lower_bound(j);
            if (it != can.begin()) l = *prev(it) + 1;
            if (next(it) != can.end()) r = *next(it);
 
            cout << (query(l, N) < r ? "YES\n" : "N/A\n");
        }
    }
}

풀이

• 각 키와 그에 맞는 도어에 대해 키 -> 도어 순서로 되어있지 않으면 NO

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        string s;
        cin >> s;
        set<int> key;
 
        bool answer = true;
        for (auto e: s) {
            if ('a' <= e && e <= 'z') {
                key.insert(e);
            } else {
                if (!key.count(e - 'A' + 'a')) {
                    answer = false;
                    break;
                }
            }
        }
 
        if (answer) {
            cout << "YES\n";
        } else {
            cout << "NO\n";
        }
    }
}

풀이

• 피보나치 수열이 증가수열이므로 내림차순으로 순열을 정렬하면 뭔가 되지 않을까부터 생각
• 맨 뒤의 1을 앞으로 하나씩 옮기면 된다.
• $[N, N - 1, ... 2, 1], [N, N - 1, ..., 1, 2], ..., [1, N, N - 1, ..., 2]$

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        int N;
        cin >> N;
 
        vector<int> a(N - 1);
        for (int i = 0; i < N - 1; ++i) {
            a[i] = i + 2;
        }
 
        sort(rall(a));
        for (int i = 0; i < N; ++i) {
            bool did = false;
            for (int j = 0; j < N; ++j) {
                if (!did && i == j) {
                    cout << "1 ";
                    did = true;
                } else {
                    cout << a[j - did] << ' ';
                }
            }
            cout << '\n';
        }
 
    }
}

풀이

• 길이 1, 2, ..., N 부분수열에 대해서 길이에 대한 maxSum 값을 구해둔다
• 그 maxSum 부분 수열의 원소들에 최대한 X 를 더하는게 이득
• 곱하는 위치수 k 에 대한 길이 d 부분수열의 합의 최댓값은 $maxSum[d] + min(d, k), * X$  

코드

• 시간복잡도: $O(N^2)$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        int N, X;
        cin >> N >> X;
        vector<long long> a(N);
        vector<long long> pa(N, 0);
        for (int i = 0; i < N; ++i) {
            cin >> a[i];
            pa[i] = a[i];
            if (i) pa[i] += pa[i - 1];
        }
 
        vector<long long> maxSum(N + 1, -1e18);
 
        maxSum[0] = 0;
        for (int d = 1; d <= N; ++d) {
            long long maxSum_ = -1e18;
            for (int i = 0; i + d - 1 < N; ++i) {
                long long sum = pa[i + d - 1];
                if (i) sum -= pa[i - 1];
                maxSum_ = max(maxSum_, sum);
            }
            maxSum[d] = maxSum_;
        }
 
        for (int k = 0; k <= N; ++k) {
            long long answer = 0;
            for (int d = 0; d <= N; ++d) {
                answer = max(answer, maxSum[d] + 1LL * min(d, k) * X);
            }
            cout << answer << ' ';
        }
        cout << '\n';
    }
}

풀이

• 각 칸에 대해서 가장 마지막으로 행한 operation 의 번호를 매기고 모든 칸에서 distinct 한 operation 번호의 수를 p 라 하면 각 p 개의 그룹에 색의 개수 k 개씩 칠하는 경우가 있으므로 답은 $k^p$ 이다
• operation 의 역순으로 생각해보자
  • 이전에 칠해진거 밑에 칠해진다
  • 다 채워진 뒤에는 더 이상 칸들의 마지막 operation 번호에 변화가 있을 수 없다.
• $r[x], c[y]$ 각각 x행/y열 이 이미 다른 번호에의해 칠해졌는가 라고 정의하면
  • 지금 수행할 operation 의 x, y 에 대해
    • r[x] = true && c[y] = true 이면 변화가 없음
    • 하나라도 false 면 가능
    • 또한 전체행이나 전체열이 채워지면 더 해볼 필요가 없음

코드

• 시간복잡도: $O(Q)$
• 주의할점: testcase 에 대한 n, m 의 제한이 없어서 testcase 마다 vector r, c 를 잡으면 이거때문에 시간초과남

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    
    int TC; cin >> TC;
 
    vector<int> r(2e5 + 1, -1), c(2e5 + 1, -1);
    while (TC--) {
        int N, M, K, Q;
        cin >> N >> M >> K >> Q;
 
        vector<pair<int, int> > operation(Q);
        for (int i = 0; i < Q; ++i) {
            cin >> operation[Q - 1 - i].first >> operation[Q - 1 - i].second;
        }
 
        int rr, cc;
        rr = cc = 0;
        long long answer = 1;
        long long MOD = 998244353;
        for (auto [x, y]: operation) {
            if (rr == N || cc == M) break;
            if (r[x] == TC && c[y] == TC) continue;
            answer = answer * K % MOD;
            if (r[x] != TC) r[x] = TC, rr++;
            if (c[y] != TC) c[y] = TC, cc++;
        }
 
        cout << answer << '\n';
    }
}

풀이

• 움직이는 칸의 범위는 처음 R, 처음 D 를 duplicate 한 칸들로 둘러 싸여있는 형태
  • 한 종류만 있는 경우에는 그냥 N
• 칸 범위 구하기
  1. 초기 칸 수
  2. 아래로 한칸씩 내릴때(duplicate D) 추가되는 칸 수(정사영 내렸을때 칸 수) * (내릴 수 있는 칸 수)
     • 추가되는 칸 수 계산할 때 처음 R, D 에 유의
  3. 아래로 다 내린상태에서 옆으로 옮길때 추가되는 칸 수 * 옆으로 옮길수 있는 칸 수

코드

• 시간복잡도: $O(s.size())$

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        long long N;
        cin >> N;
        string s;
        cin >> s;
 
        long long r, d, fr, fd;
        r = d = fr = fd = 0;
 
        for (int i = 0; i < s.size();) {
            if (s[i] == 'R') {
                int tmp = 0;
                while (i < s.size() && s[i] == 'R') ++tmp, ++i;
                r += tmp;
                if (fr == 0) fr += tmp;
            } else {
                int tmp = 0;
                while (i < s.size() && s[i] == 'D') ++tmp, ++i;
                d += tmp;
                if (fd == 0) fd += tmp;
            }
        }
 
        if (r == 0 || d == 0) {
            cout << N << '\n';
            continue;
        }
        
        long long answer = 0;
        if (s[0] == 'D') {
            answer = (r + d + 1);
            answer += (r + 1) * (N - d - 1);
            answer += (d - fd + 1 + N - d - 1) * (N - r - 1);
        } else {
            answer = (r + d + 1);
            answer += (r - fr + 1) * (N - d - 1);
            answer += (d + 1 + N - d - 1) * (N - r - 1);
        }
        cout << answer << '\n';
    }
}

풀이

• 배열 원소들의 or 값은 일정
• 0 아닌 두 수를 0 과 $a_i$ $|$ $a_j$ 로 바꾸자

코드

#include <bits/stdc++.h>
 
using namespace std;
 
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
 
int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int TC; cin >> TC;
    while (TC--) {
        int N;
        cin >> N;
        vector<long long> a(N);
        long long answer = 0;
        for (auto& e: a) {
            cin >> e;
            answer |= e;
        }
        cout << answer << '\n';
    }
}