문제링크
https://www.acmicpc.net/problem/3640
3640번: 제독
두 함선(빨강, 파랑)은 1에서 시작해서 6에서 만난다. 빨간 함선은 1 → 3 → 6 (총 33개 포탄)으로 이동하고, 파란 함선은 1 → 2 → 5 → 4 → 6 (총 53개 포탄)으로 이동한다. 두 경로에서 출발
www.acmicpc.net
풀이
- 시작점에서 끝지점까지 최대 용량을 2로 해두고 MCMF 해주기
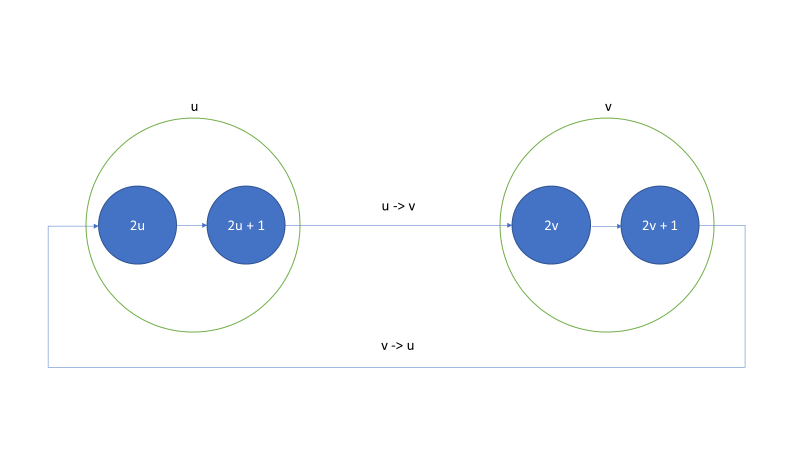
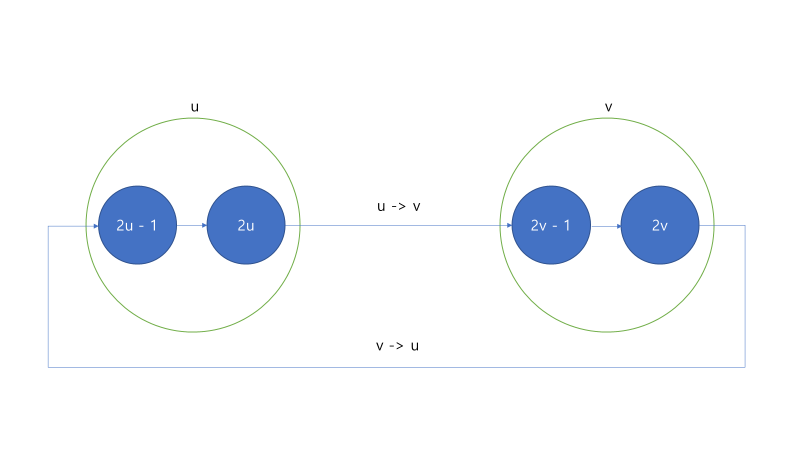
- 두 경로사이에 겹치는 정점, 간선 없게하기위해 각 정점 한번씩만 지날 수 있도록 -> 정점분할
- v : 2v - 1 -> 2v
코드
- 시간복잡도: $O((V+E)f) = O(V+E)$
#include <bits/stdc++.h>
using namespace std;
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
struct Edge {
int to, c, f, cost;
Edge* reverse;
Edge() {
to = c = f = cost = 0;
reverse = nullptr;
}
Edge(int to_, int c_, int cost_) {
to = to_;
c = c_;
cost = cost_;
f = 0;
reverse = nullptr;
}
int reisidual() {
return c - f;
}
};
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int v, e;
while (cin >> v >> e) {
int S = 1;
int T = 2 * v - 1;
vector<vector<Edge*> > adj(2 * v + 1);
auto makeEdge = [&](int u, int v, int c, int cost) {
auto e1 = new Edge(v, c, cost);
auto e2 = new Edge(u, 0, -cost);
e1 -> reverse = e2;
e2 -> reverse = e1;
adj[u].push_back(e1);
adj[v].push_back(e2);
};
while (e--) {
int u, v, c;
cin >> u >> v >> c;
makeEdge(2 * u, 2 * v - 1, 1, c);
}
makeEdge(1, 2, 2, 0);
for (int i = 2; i <= v; ++i) {
makeEdge(2 * i - 1, 2 * i, 1, 0);
}
int maxFlow = 0;
int minCost2 = 0;
while (true) {
vector<Edge*> prev(2 * v + 1, nullptr);
queue<int> q;
vector<int> inQ(2 * v + 1, false);
vector<int> minCost(2 * v + 1, 1e9);
q.push(S);
minCost[S] = 0;
inQ[S] = true;
while (q.size()) {
int cur = q.front();
q.pop();
inQ[cur] = false;
for (auto e: adj[cur]) {
if (e -> reisidual() > 0 && minCost[e -> to] > minCost[cur] + e -> cost) {
minCost[e -> to] = minCost[cur] + e -> cost;
prev[e -> to] = e;
if (!inQ[e -> to]) {
q.push(e -> to);
inQ[e -> to] = true;
}
}
}
}
if (!prev[T]) break;
int flow = 1e9;
for (auto cur = T; cur != S; cur = prev[cur] -> reverse -> to) {
flow = min(flow, prev[cur] -> reisidual());
}
for (auto cur = T; cur != S; cur = prev[cur] -> reverse -> to) {
prev[cur] -> f += flow;
prev[cur] -> reverse -> f -= flow;
}
maxFlow += flow;
minCost2 += minCost[T];
}
cout << minCost2 << '\n';
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 1605번: 반복 부분문자열 (0) | 2022.03.07 |
|---|---|
| 백준 11479번: 서로 다른 부분 문자열의 개수 2 (0) | 2022.03.07 |
| 백준 13263번: 나무 자르기 (0) | 2022.03.06 |
| 백준 4008번: 특공대 (0) | 2022.03.06 |
| 백준 16978번: 수열과 쿼리 22 (0) | 2022.03.02 |